En RF-signal, i form av en växelström, oscillerar ständigt mellan positiv och negativ spänning. Våglängden är avståndet mellan två på varandra följande vågtoppar eller vågdalar i ett vågmönster. Med andra ord representerar en våglängd den sträcka som en RF-signal färdas under en enda cykel.

Begreppet ”cykel” refererar till en fullständig svängning eller oscillation av vågen. Det motsvarar en komplett upprepning av vågens mönster från en vågtopp till nästa vågtopp eller från en vågdal till nästa vågdal. I grund och botten är en cykel en komplett period av vågens form, och det kan vara ett användbart begrepp för att mäta tidsperioden eller avståndet mellan två liknande punkter på en våg. I elektriska och elektromagnetiska vågor, såsom radiovågor, representerar en cykel en hel svängning mellan positiva och negativa spänningstoppar inom en växelströmsignal.

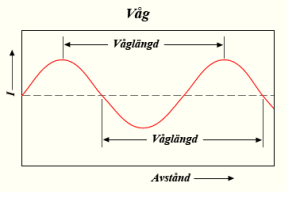
Radiovågor har varierande våglängder beroende på deras frekvens. Som sagt, våglängden är avståndet mellan två på varandra följande vågtoppar (eller vågdalar) i en vågcykel. För radiovågor varierar våglängden från långa avstånd till korta avstånd beroende på frekvensen. Här är några exempel på radiovågors våglängder:

• FM-radio (frequency modulation): FM-radiovågor har frekvenser som sträcker sig från ca 88 MHz till 108 MHz. Deras våglängder varierar därför från ungefär 2,8 meter till 3,4 meter.
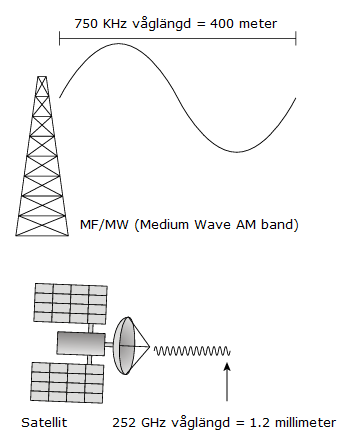
• AM-radio (amplitude modulation): AM-radiovågor har lägre frekvenser, vanligtvis i området 540 kHz till 1700 kHz. Därmed har de längre våglängder, som sträcker sig från 176 meter till 555 meter.
• Mikrovågor: Mikrovågor, som används i exempelvis mikrovågsugnar och trådlös kommunikation som Wi-Fi och mobiltelefoni, har högre frekvenser. Deras våglängder varierar från millimeter till centimeter. Till exempel har 2,4 GHz Wi-Fi-signaler våglängder på cirka 12,5 centimeter och %,0 GHz på ca 6 centimeter..

RF-signaler används inom trådlös kommunikation tack vare deras förmåga att sprida sig med ljusets hastighet (299 792 458 m/s). Radiovågor har våglängder (λ) som sträcker sig från 1 mm till 1000 km och frekvenser (f) som sträcker sig från 300 Hz till 300 GHz. Radiosändningar utförs inom frekvensområden på 10 kHz till 500 MHz.

Det är viktigt att notera att längre våglängder inte nödvändigtvis betyder lägre frekvenser och vice versa. Våglängd och frekvens är omvända proportionella till varandra enligt relationen c = fλ, där c är ljusets hastighet, f är frekvensen och λ är våglängden. Exempelvis:

• Frekvensområdet 300 GHz till 430 THz resulterar i våglängder på 700 till 380 nm.
• Frekvensområdet 30 KHz till 3 GHz ger våglängder på 1 km till 10 cm.

Radiovågors matematiska grunder

Egenskaperna hos elektromagnetiska vågor, såsom våglängd, frekvens, utbredningshastighet och periodtid, är inbördes relaterade och matematiskt uttryckta i referensformeln:  c =  λ* f m/s och f = 1 / T

Denna referensformel kan omformuleras till f = c / λ.  och  λ = c / f

• Frekvens ( f)uppmätt i Hertz (Hz)
• Våglängd (λ) mätt i meter (m)
• Ljusets hastighet (c) är en konstant på 300 000 000 m / s.
• När man beräknar våglängder, använder man den avrundade ljusets hastigheten på 300 000 000 m/s och frekvensen i Hz (per sekund) eller 300 000 km/s och frekvenser i kHz (per sekund), vilket ger våglängden i meter. 

Exempel på användning av referensformel:

Exempel 1: Beräkna våglängden för en radiovåg med en frekvens på 100 MHz.

• Frekvens (f) = 100 MHz = 100 000 000 Hz
• Ljusets hastighet (c) = 300 000 000 m/s
• λ = c / f = 300 000 000 m/s / 100 000 000 Hz = 3 meter

Så våglängden för en radiovåg med en frekvens på 100 MHz är 3 meter.

Exempel 2: Beräkna frekvensen för en radiovåg med en våglängd på 10 cm.

• Våglängd (λ) = 10 cm = 0.1 meter
• Ljusets hastighet (c) = 300 000 000 m/s
• f = c / λ = 300 000 000 m/s / 0.1 meter = 3 000 000 000 Hz = 3 GHz

Så frekvensen för en radiovåg med en våglängd på 10 cm är 3 GHz.

Exempel 3: Beräkna våglängden för en radiovåg med en frekvens på 5 GHz.

• Frekvens (f) = 5 GHz = 5 000 000 000 Hz
• Ljusets hastighet (c) = 300 000 000 m/s
• λ = c / f = 300 000 000 m/s / 5 000 000 000 Hz = 3/5 m = 0.06 meter = 6 cm

Så våglängden för en radiovåg med en frekvens på 5 GHz är 6 cm.

Dessa exempel visar hur våglängd och frekvens är omvänt proportionella och hur de beräknas med hjälp av ljusets hastighet och varandra.