Den grundläggande definition av decibel är en relativ enhet som är relaterad till ett förhållande mellan två värden, in och ut. Detta kan illustreras med bilden nedan som effekt in, effekt ut (Power):

Den gröna lådan föreställer en förstärkare med namn A. Förhållande mellan in och ut signaler kan härledas matematiskt så här:
Det matematiska uppställning ovan kan tolkas som A visar förhållande mellan effekt ut jämförd med effekt in, men A är enhetslös. För att ge A en enhet behöver vi enheten bel.
Att ge A enheten bel (B) kan göras matematiskt så här:
Nu har A fått enheten bel (B). Men vad händer om in-effekt och uteffekt är lika? Då innebär det att inget har ändrats och att insignalen är lika stark som utsignalen.
Så ingen förändring är noll bel (0 B).
Vad händer om uteffekten blir 10 gånger starkare en in-effekten? Detta kan tolkas som in-effekt är lika stor som uteffekt men 10 gånger större.
Det innebär att 1 bel är egentligen en förändring med faktorn 10!
- 1 B = 10 ggr skillnad
- 2 B = 10 * 10 = 100 ggr skillnad
- 3 B = 10*10*10 = 1000 ggr skillnad
Här finns möjlighet att inkludera 10 i formeln och då får vi decibel istället!
När ingen förändring sker mellan in- och uteffekt har vi sett att det motsvarar 0 B. Det samma sker med decibel där ingen förändring/skillnad är 0 dB.
Användning av decibel
I trådlös kommunikationsteknik används flitigt decibel begreppet just för att beskriva skillnader mellan antennernas in och uteffekt. Till exempel in-effekt på 0,1 W har blivit uteffekt på 50 W. Hur beskriver vi skillnaden matematiskt ? Det är uppenbart att den tiondels Watt har blivit 50 Watt, men hur kan skillnaden uttryckas och betecknas?
Skillnaden kan betecknas som 27 dB, men den ger inte skillnadens dimensionen. Vi behöver tolka vad 27 dB betyder. Vi utgår från att decibel är en relativ enhet och att decibel används vid jämförelser. När man jämför något med något annat behöver man en referens och några regler:
- 0 dB ger ingen skillnad vilket kan också uppfattas som ingen förändring.
- +3 dB är dubbel så mycket än referensen
- -3 dB är hälften så mycket än referensen
- +10 dB är tio gånger så mycket än referensen
- -10 dB är en tiondel så mycket än referensen
Nu bygger vi upp en enkel tabell som kommer att underlätta beräkningar, ungefär som multiplikationstabellen vi lärde oss i grundskolan.
| dB värde | Skillnad |
| 60 | 1 000 000 |
| 50 | 100 000 |
| 40 | 10 000 |
| 30 | 1 000 |
| 20 | 100 |
| 10 | 10 |
| 9 | 8 |
| 6 | 4 |
| 3 | 2 |
| 0 | 1 |
Nu kan vi tolka 27 dB.
- Ur tabellen är 30 dB = 1000 ggr och då kan vi dra av 3 dB vilket innebär att skillnaden halveras.
- 27 dB = 500 Detta säger till oss att uteffekten är 500 ggr starkare än in-effekten.
Ett exempel till:
Antag att vi har 3 förstärkare A1, A2, och A3 (se bilden nedan). Antag också att in-effekt är 0,1 mW
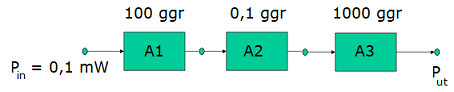
Hur stor blir uteffekten?
Så 0,1 mW har blivit 1 W. Nu beräknar vi i decibel så att vi kan beskriva skillnaden.
Det som är viktig här är förstärkarnas värde, det vill säga 100 ggr = 20 dB, 0,1 ggr är en tiondel = -10 dB, och 1000 ggr = 30 dB sätter vi ihop dem:
20 + (-10) + 30 = 40 dB och 40 dB = 10000 ggr
Uteffekten är 10 000 ggr starkare än in-effekten.